Binomial distribution

$p(x)=C_k^nn^p(n-k)^{(1-p)}=\frac{n!}{k!(n-k)!}p^k(1-p)^{(n-k)}$

$\begin{aligned} E(x)&=\sum_{k=1}^{n}k\frac{n!}{k!(n-k)!}p^k(1-p)^{(n-k)} \\ &= \sum_{k=1}^{n}k\frac{n(n-1)!}{k(k-1)!(n-k)!}p p^{k-1}(1-p)^{(n-k)} \\ &= np\sum_{k=1}^{n}\frac{(n-1)!}{(k-1)!(n-k)!}p^{k-1}(1-p)^{(n-k)} \end{aligned}$

Let $a = k-1$ , $b=n-1$ $\Rightarrow k=a+1, n=b+1$

$\begin{aligned} E(x)&= np\sum_{k=1}^{n}\frac{(n-1)!}{(k-1)!(n-k)!}p^{k-1}(1-p)^{(n-k)} \\ &= np\sum_{a=0}^{b}\frac{b!}{a!(b-n)!}p^{a}(1-p)^{(b-a)} \end{aligned}$

Where $\sum_{a=0}^{b}\frac{b!}{a!(b-n)!}p^{a}(1-p)^{(b-a)}$ is the sum of all the probabilities which equals to 1.

Hence the $E(x)$ is $np$

Combination and Permutation

When the order doesn’t matter, it is a Combination.
When the order does matter it is a Permutation.

A Permutation is an ordered Combination.

lock

This is a Permutation Lock.

熵

向空中投掷硬币，落地后有两种可能的状态，一个是正面朝上，另一个是反面朝上，每个状态出现的概率为1/2。如投掷均匀的正六面体的骰子，则可能会出现的状态有6个，每一个状态出现的概率均为1/6。试通过计算来比较状态的不肯定性与硬币状态的不肯定性的大小。

H(硬币)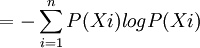 $= -\sum^{n}_{i=1}P(Xi)log P(Xi)$

= -(2×1/2)×logP2(1/2)≈1(比特)

H(骰子)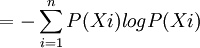 $= -\sum^{n}_{i=1}P(Xi)log P(Xi)$

= -6×(1/6)×logP2(1/6)≈2.6(比特)

由以上计算可以得出两个推论：

[推论1] 当且仅当某个P(Xi)=1，其余的都等于0时， H(X)= 0。

[推论2]当且仅当某个P(Xi)=1/n，i=1， 2，……， n时，H(X)有极大值log n。

经验

树模型对于缺失值的敏感度较低，大部分时候可以在数据有缺失时使用。基于特征采样的统计分布的方法对缺失值有更高的抗性。
涉及到距离度量(distance measurement)时，如计算两个点之间的距离，缺失数据就变得比较重要。因为涉及到“距离”这个概念，那么缺失值处理不当就会导致效果很差，如K近邻算法(KNN)和支持向量机(SVM)。
线性模型的代价函数(loss function)往往涉及到距离(distance)的计算，计算预测值和真实值之间的差别，这容易导致对缺失值敏感。
神经网络的鲁棒性强，对于缺失数据不是非常敏感，但一般没有那么多数据可供使用。
贝叶斯模型对于缺失数据也比较稳定，数据量很小的时候首推贝叶斯模型。

数据库

数据库事务四大特性:

1、原子性（Atomicity）

原子性是指事务包含的所有操作要么全部成功，要么全部失败回滚，因此事务的操作如果成功就必须要完全应用到数据库，如果操作失败则不能对数据库有任何影响。

2、一致性（Consistency）

一致性是指事务必须使数据库从一个一致性状态变换到另一个一致性状态，也就是说一个事务执行之前和执行之后都必须处于一致性状态。

拿转账来说，假设用户A和用户B两者的钱加起来一共是5000，那么不管A和B之间如何转账，转几次账，事务结束后两个用户的钱相加起来应该还得是5000，这就是事务的一致性。

3、隔离性（Isolation）

隔离性是当多个用户并发访问数据库时，比如操作同一张表时，数据库为每一个用户开启的事务，不能被其他事务的操作所干扰，多个并发事务之间要相互隔离。

即要达到这么一种效果：对于任意两个并发的事务T1和T2，在事务T1看来，T2要么在T1开始之前就已经结束，要么在T1结束之后才开始，这样每个事务都感觉不到有其他事务在并发地执行。

4、持久性（Durability）

持久性是指一个事务一旦被提交了，那么对数据库中的数据的改变就是永久性的，即便是在数据库系统遇到故障的情况下也不会丢失提交事务的操作

索引是对数据库表中一个或多个列的值进行排序的数据结构，以协助快速查询、更新数据库表中数据。

索引的特点：
创建索引的好处
（1）通过创建索引,可以在查询的过程中,提高系统的性能
（2）通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性
（3）在使用分组和排序子句进行数据检索时,可以减少查询中分组和排序的时间
创建索引的坏处
（1）创建索引和维护索引要耗费时间,而且时间随着数据量的增加而增大
（2）索引需要占用物理空间,如果要建立聚簇索引,所需要的空间会更大
（3）在对表中的数据进行增加删除和修改时需要耗费较多的时间,因为索引也要动态地维护