Optimization

Gradient Descent

Batch Gradient Descent(BGD)

Let data has $n$ observations, model has parameter $\theta$, loss function as $J(\theta)$, the gradient at point $(x_i,y_i)$ is $\bigtriangledown_\theta J(\theta_t,x_i,y_i)$, learning rate is $\eta$. Then we have the formula:

$\theta_{t+1}=\theta_t-\eta_t\sum_{i=1}^{n}\bigtriangledown_\theta J(\theta_t,x_i,y_i)$

So everytime we update our parameter, we need to compute whole data. Then this method is slow for large data size. But everytime it caculates the average gradient of whole data, the result is global optimization.

Stochastic Gradient Descent(SGD)

Not like BGD, every time it only use one data to caculate the gradient:

$\theta_{t+1}=\theta_t-\eta_t\bigtriangledown_\theta J(\theta_t,x_i,y_i)$

SGD is fast but easy to lead to a local optimization which means the accurate is decreased.

Min-batch Gradient Descent

Combine teh BGD abd SGD, it used a subset of data to do the update. We have $x$ times update and we select a subset size as $m$ where $m<n$

$\theta_{t+1}=\theta_t-\eta_t\sum_{i=x}^{x+m-1}\bigtriangledown_\theta J(x_i,y_i,\theta_t)$

When we have small dataset, we better use BGD. And in large dataset, we may use SGD or MBGD.

Least Square Method

Newton Method

For the target function $f(x)$: we find the Taylor Expression

$f(x) = f(x_0) + \bigtriangledown f(x_0)^T(x-x_0) + \frac{1}{2} \bigtriangledown^2 f(x_0)(x-x_0)+ ...$

Calculating the gradient for both side and ignore the $\bigtriangledown^2$ above elements:

$\bigtriangledown(x) = \bigtriangledown f(x_0) + \bigtriangledown ^2 f(x_0)(x-x_0)$

And we let $\bigtriangledown (x) = 0$ and denote $\bigtriangledown ^2 f(x_0)$ as Hessian matrix $H$

$\bigtriangledown f(x_0) + H(x-x_0) =0$

$x = x_0 - H^{-1} \bigtriangledown f(x_0)$

So we start from $x_0$, repeate calculate the $x_{k+1} = x_k - H_k^{-1} \bigtriangledown f(x_k)$ until $\bigtriangledown f(x_k)$ almost equal to 0

Quasi-Newton Method

Calculating the Hessian matrix every time cost a lot of computation. So there are many methods which find a similar Hessian matrix to finish the loop.

AdaGrad

It adjusted the learning rate for the different gradient at each features. Avoiding the same learning rate hard to fit all features.

Here is the function to update the parameter:

$\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\varepsilon I + diag(G_t)}} \cdot g_t$

Where

• $\theta$ is the parameter need to be updated
• $\eta$ Is the initial learning rate
• $\varepsilon$ is the some small quantity that used to avoid the division is 0
• $I$ is the identity matrix
• $g_t$ is the gradient estimate at time $t$

$g_t = \frac{1}{n} \sum_{i=1}^{n} \bigtriangledown_\theta J(x_i, y_i, \theta_t)$

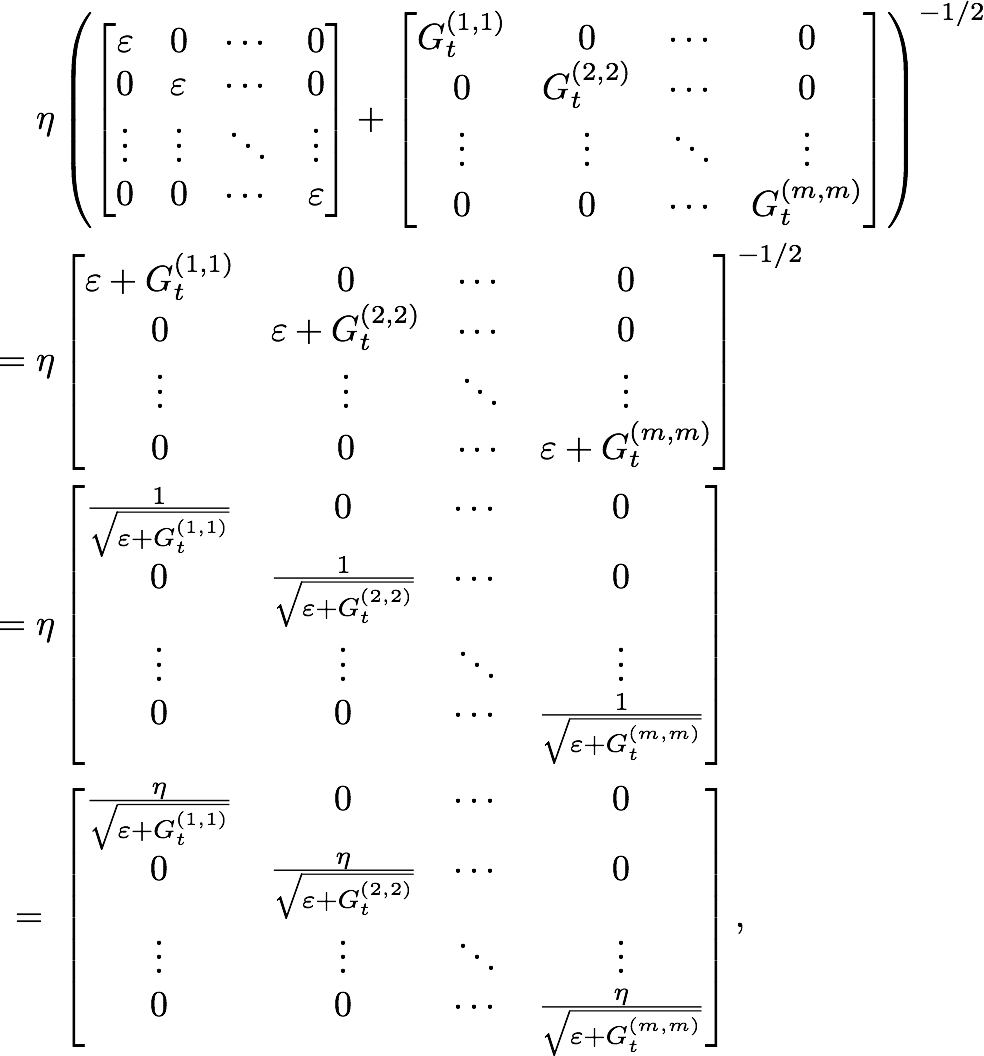
• $G_t$ Matrix is the key point which is teh sum of the outer product of the gradients until time-step $t$

  $G_t = \sum_{\tau=1}^{t}g_{\tau}g_{\tau}^T$

  Note that we can use full $G_t$ matrix but it is impractical especially in high-dimension problem. Hence we use the inverse the square root of the diagonal $G_t$ is easier to be computed.

Rewritting the AdaGrad function into matrix form:

multiply $g_t$

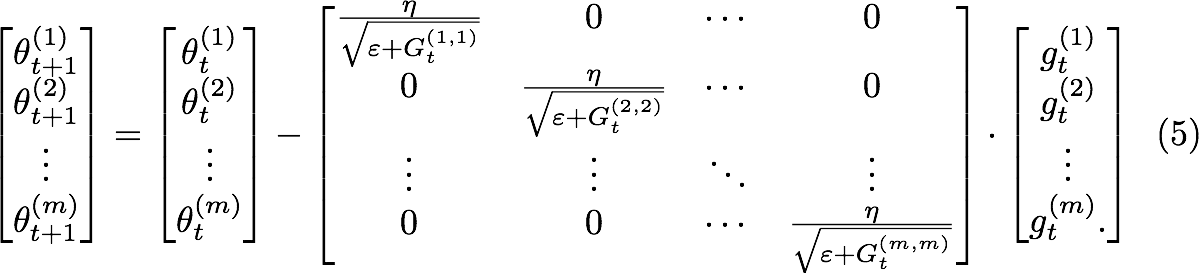
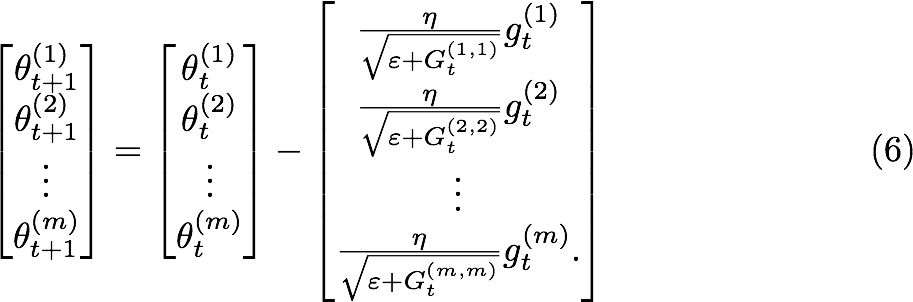
compare to the SGD(stochastic gradient descent)

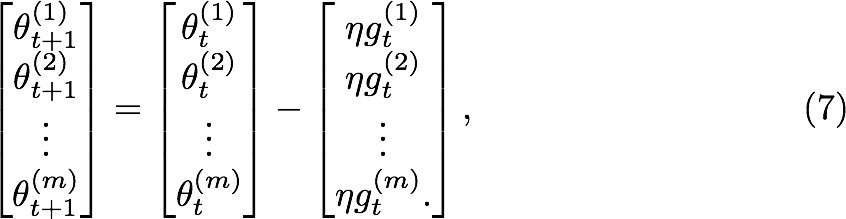
Where SGD used the same learning rate for each dimension. AdaGrad adapt the learning rate with the accumulated squared gradient at each iteration in each dimension.

AdaGrad algorithm performs best for sparse data because it decreases the learning rate faster for frequent parameters, and slower for parameters infrequent parameter. Unfortunately, there is some case that the effective learning rate `decreased very fast because we do accumulation of the gradients from the beginning of training. This can cause an issue that there is a point that the model will not learn again because the learning rate is almost zero.